As most photographers know, in you increase the distance between the lens and camera to do close-ups, the exposure must also be increased. I never had to worry about this much in 35mm because I always had a TTL meter to use. This has changed with large format (LF). Long bellows and no meter meant I had to do the calculations manually. After considerable searching for an easy method, I've come up with a few I'd like to share. Why? Because what I read in the newsgroups and web sites make it all very much too complicated... I've described the 'standard' calculations here because they're in the books I own. Most of the ones I've read in the newsgroups are just to complicated to remember... Also see the new calculator at the bottom of this page!

First, the 'standard' calculation.

EF = (m + 1)^2

where EF = exposure factor (same as for filters)

m = magnification

^2 = squared

It's a simple formula, but what's the magnification? I suppose you could use a ruler to measure the size of your subject and then compare it to the size it appears on the ground glass? There's also a way of calculating magnification using the lens length, distance to lens from subject, bellows extension, etc... Never mind... Way too much work and calculating...

The next formula is EF = d^2/f^2

where EF = exposure factor

d^2 = distance from the lens diaphragm to film plane, squared.

f^2 = focal length of the lens, squared.

This is a bit easier because you don't have to figure out the magnification. This formula works well. However, I never could figure out why d and f have to be squared first, making mental calculations very difficult (for me anyway). Do the division first, then square the result. EF will be the same and it's a lot easier to do mentally. So the new formula is:

EF = ( d / f )^2

Okay, for me that is easier but still difficult without writing something down.

Then I found the formula I now use. In "Close-up Photography" written for Kodak by William White, Jr. (a Kodak Workshop Series book) a 'new' formula is presented that I find much easier. See Special Note below!

s = ( 2 / f ) * x

where

s = f-stops to increase.

f = focal length of the lens.

x = bellows extension.

To try and make this a bit clearer. This formula works directly in f-stops, not exposure factors. This eliminates one calculation already! The focal length of the lens can be either in inches or millimeters! The bellows extension is measured as an extension beyond infinity focus. That means if you are using a 6 inch lens, you would start measuring at the six inch mark up to the lens diaphragm. Or measure the total bellows extension from the film plane and then subtract the six inches of lens. For an example:

a six inch lens is focused using 12 inches of bellows.

( 2 / 6 ) * 6 = 2

The ( 2 / 6 ) is simply 2 divided by the lens length in inches equal to 1/3.

* 6 is the bellows extension. 12 inches of bellows minus a 6 inch lens equals 6.

The result is a 2 f-stop increase directly in f-stops, not exposure factors.

If this formula is used in millimeters with the lens, then the bellows extension must also be measured in millimeters! I use a three foot tape measure from a fabric store. It's vinyl coated fiberglass, very strong, reads both in inches and millimeters and cost me 99 cents! I remember the formula simply as "two over the lens times the extension" and it gives me the f-stop increase. It's the simplest and easiest to remember I have yet found and I can do it mentally without writing anything down.

Special note: After creating my own exposure calculator (see below) and having to do quite a few calculations to get all those numbers, I realised there was something wrong with this last formula. It works fine up to 1:1 and close up to 1.5:1, but then fails miserably. Here's another example:

Here's the problem. This equates to 1.5:1 (150%) magnification. Using the first formula at the top of this page, we would get a correction factor of 6.25. EF = (m + 1)^2 or 6.25=(1.5+1)^2.. This is equal to only 2.6 stops, not 3!
Using the second formaul EF = ( d / f )^2: 6.25=(15/6)^2, exactly the same result.
The discrepancy gets worse as the magnification increases.
Now, I didn't make this formula up and did like it very much until I found out this problem. It is fully explained on page 41 of "Close-up Photography", 'the Kodak Workshop Series'. If I'm somehow interpreting this wrong or completely messed up something, I'd sure like to know about it. But for right now, the first two formulas agree, and so does the Calumet calculator (and my own ;-) which makes the thrid formula look pretty suspect. I wouldn't recommend using it. I leave all this here just in case I did something wrong, or someone else buys this book and wants to use this formula...

One other note. This gives an f-stop increase. When I shoot extreme close-ups I use all the arperture I can get. f-32, f-64, whatever the lens will give me for depth of field. I won't give up even a stop for the exposure increase. So simply exchange it for time in the final exposure. For every stop, you multiply the time by two...

What to do with the formulas that give correction factors instead of f-stops? Very simple, just multiply your time by the correction factor. This works for any speed, but you have to pay attention to the fraction above 1 second. For long exposures it's a simple multiply. Say an original time of 5 seconds with an exposure factor of 8. Multiply 5 times 8 to get 40 seconds for the new time. If you doubt it, 8 = 3 stops. Double the time for every stop. 5->10->20->40.

For fractional time, shorter than 1 second, this still works but takes a little bit more work and an acceptance of non-standard math for shutter speeds ( 1/60 is not half of 1/125, but it is!). So if your original time is 1/250, then the new time would be 8/250. If you do actual math, the numbers won't come out right. Although it would be close at 1/31.25 or 1/30 in photo-math. Take it down the easy way by dividing both top & bottom number by 2's. 8/250 -> 4/125 -> 2/60 -> 1/30. When you reach 1 at the top, you're done, and notice the photo-math between 4/125 and 2/60... It's simpler to do than explain...

And don't forget about reciprocity failure! Simply put, there is a point where the film needs more exposure time than shown on a meter to correctly register the light. This usually starts between 1 and 10 seconds. Correction can be as much a 4 times the indicated exposure. Correction for reciprociy failure can be found in film's instruction sheets or the data sheets availble from the manufacturers..

If your mental math isn't up to the job, and sometimes mine isn't ;-) There's a very workable and affordable solution. I have tried the Calumet Exposure Calculator and it works just fine. It's under $8.00 directly from Calumet (see my dealer listing ) and comes in a nice little clear plastic sleeve for protection and keeps the two parts together. It consists of a 2 inch plastic square, white on one side and black on the other with a contrasting cross through both sides. You simply put this square on your subject and then use the second piece, a ruler of sorts, to measure the square on the ground glass. This has two scales. One reads directly in f-stops for exposure increase, up to 3 1/2 stops. The other reads magnification in percent, up to 250%. It works well, is handy & water proof. The only problem is placing the square on the subject. It must be fairly square to the camera and held somehow. For some subjects this could be difficult (delicate flowers). But I do recommend this device as well worth the investment for those days when the brain just doesn't want to do the math...

I know there's a lot more formulas out there and a host of other ways to do the calculations as I've seen in the newsgroups. Many photographers use the "for every inch of bellows increase so many stops". They always fail to mention the difference between lenses.

Another general rule worth remembering is the "increase exposure any time you focus less than 8 times the focal length of the lens". It sounds long, but easy to remember. A six inch lens times 8 would be 48 inches. So if you focus closer than 48 inches, or 4 feet, you would have to calculate a new exposure due to bellows extension. For me, these two methods (the above recommended calculation and the calumet Exposure Calculator) have worked out to be the easiest to use and remember...

---

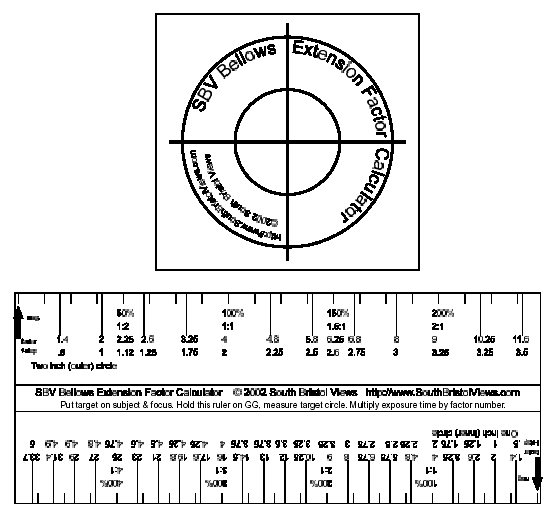
The SBV Bellows Extension Factor Calculator

I mentioned the Calumet Exposure Calculator up there, and I do use it and like it. But it has a few drawbacks that bother me now and then. So I've decided to make my own. It has some advantages, may be as accurate(?), but doesn't come in plastic or with a nice protective holder...

Basically, it's the same idea as the many close-up "calculators" available commercially or free through the internet. At the moment, I like mine better for a few reasons. It has a round target making the measurment on the ground glass a bit easier. It has two sized targets that work from 0.5:1 all the way up to 4.5:1, which none of the other ones I've seen do. It has all the scales; magnification, f-stop correction, factor correction; on the same side of the 'ruler'. Give it a look. I'm making it available here for free download and use as long as it retains my copyright notice & markings, remains un-altered in any form (except of course the cutting for use) and basically I always get the credit for it's creation ;-) I am completely open to any suggestions as to improvements! I hope to refine the calculations in the near future and maybe make them a more standard 1/3 f-stop instead of the decimals as they are now. If decimal numbers throw you off, skip this and find another one for now... But let me know what you think of it and what you'd like to see changed. It's in PDF format, so you'll need some flavor of Adobe Acrobat to view/print it. Don't worry about it printing in exact dimensions because it's the relationship between the target & ruler that matters. Give it a look and let me know...

Here's what it looks like. Just click on the pic below to download the PDF version, then print it out to use. What I do to preserve the calculator & ruler because they will be printed on plain paper and probably not too water proof is: right after printing, cover the printed area on both sides with clear packing tape. This is really just very wide 'Scotch' tape, maybe a bit heavier. After taping both sides, cut out the target & ruler. Of course a laminator would be much better, but the tape lasts a couple of years in use & a whole lot cheaper...

 Send e-mail to Rich

Entire site contents
© 1999-2017 South Bristol Views

Modified on Saturday, April 04, 2015